



Next: Reduction strategies
Up: Rewriting as a model
Previous: Rewriting as a model
Contents
Let 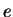 be a Haskell expression with two reductions
be a Haskell expression with two reductions
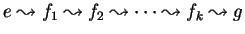 and
and
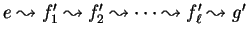 such that
such that  and
and 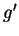 cannot be further reduced. Then,
cannot be further reduced. Then,
 .
.
In general, we need a strategy for reduction--that is, a rule
telling us how to apply the rules! Some questions we might ask are:
- Are all reduction strategies equivalent with respect to the
final result (this property is called confluence)?
- Can we tell whether the reduction process will terminate? For
example, consider what happens to the expression factorial -1
with respect to the definition
factorial:: Int -> Int
factorial n = n * (factorial (n-1))
- Given a choice of reduction strategies, can we always identify
the optimal one, in terms of efficiency? Notice in the reduction of
square (4+3) that the first reduction sequence is shorter
than the other two.
Madhavan Mukund
2004-04-29