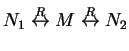 , so
, so
 . There must
then be a common
. There must
then be a common
Suppose ![]() and
and ![]() are both normal forms for
are both normal forms for ![]() . Then,
. Then,
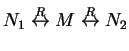 , so
, so
 . There must
then be a common
. There must
then be a common ![]() such that
such that ![]() and
and ![]() . Since neither
. Since neither
![]() nor
nor ![]() can be reduced, it follows that
can be reduced, it follows that
![]() .
.
![]()
Recall that our goal is to check whether normal forms in the lambda
calculus are unique. One way to do this is to show that
![]() has the
Church-Rosser property.
has the
Church-Rosser property.
For any relation ![]() , if
, if ![]() has the Church-Rosser
property, then so does
has the Church-Rosser
property, then so does ![]() . The proof of this is easy to
see pictorially.
. The proof of this is easy to
see pictorially.

If
![]() (the horizontal axis) and
(the horizontal axis) and
![]() (along the vertical axis), we can break up both reductions into a
sequence of individual steps. From the fact that
(along the vertical axis), we can break up both reductions into a
sequence of individual steps. From the fact that ![]() is
Church-Rosser, we can complete the diamond for each single step in the
sequence. In the end, we get a complete rectangle between
is
Church-Rosser, we can complete the diamond for each single step in the
sequence. In the end, we get a complete rectangle between ![]() and
and
![]() and the corner opposite
and the corner opposite ![]() is the common term that we can
obtain from
is the common term that we can
obtain from ![]() and
and ![]() .
.
Unfortunately, ![]() does not have the Church-Rosser property, so we
cannot use this strategy to establish that
does not have the Church-Rosser property, so we
cannot use this strategy to establish that
![]() is Church-Rosser!
Consider the term
is Church-Rosser!
Consider the term
![]() . We
have two reductions possible:
. We
have two reductions possible:
If we take the second option, we can then in one step get
We can reach this term from the first option as well, but it requires two steps!
The solution lies in defining an alternative notion of one step
reduction from the basic beta reduction
![]() such that
such that
We define this new reduction
![]() as follows.
as follows.
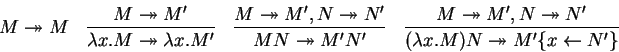
The last inference rule builds in ![]() reduction. The crux of the
relation
reduction. The crux of the
relation
![]() is that it combines nonoverlapping
is that it combines nonoverlapping ![]() reductions
in one parallel step. For instance, if both
reductions
in one parallel step. For instance, if both ![]() and
and ![]() can be
reduced to
can be
reduced to ![]() and
and ![]() , respectively, then
, respectively, then ![]() can be reduced to
can be reduced to
![]() in one step.
in one step.
We claim, without proof, that
![]() is Church-Rosser and that
is Church-Rosser and that
![]() is the same as
is the same as
![]() . Assuming the claim, it then
follows that
. Assuming the claim, it then
follows that
![]() is Church-Rosser and so the normal form for a
term in the lambda calculus is unique, if it exists.
is Church-Rosser and so the normal form for a
term in the lambda calculus is unique, if it exists.